FST Algorithms
Determine
A weighted automaton is said to be deterministic or subsequential if it has a unique initial state and if no two transitions leaving any state share the same input label.
Compose
FST的compose操作用于组合不同层次的信息。低层次(细粒度)的FST A可以通过和高层次的(粗粒度)的FST B进行compose操作,生成输入为低层次(细粒度),输出为高层次(粗粒度)的FST C. 即 C = A * B,其中*表示compose操作。例如在语音识别任务中,最终生成的解码图为HCLG,H/C/L/G分别表示不同层级的FST,其中:
- H表示HMM层级的FST,输入为senone状态,输出为context-dependent phone。
- C表示Context层级的FST,语音识别中的音素建模时考虑当前音素的上一个音素和下一个音素,即输入为context-dependent phones,输出为phone。
- L表示Lexicon层级的FST,对单个的词来讲,输入为该词的phone序列,输出为该词。
- G表示Grammar层级的FST,一般Grammar指语言模型,是将arpa的语言模型表示为等价的FST的形式,输入输出均为词。
可以看到,从H->C->L->G,低层次的FST的输出粒度刚好对应高一层次FST的输入粒度,通过compose H*C*L*G,即可将HMM/Context/Lexicon/Grammar所有层次的信息构建在一个FST HCLG中,该HCLG输入为语音识别声学模型的建模单元senone,输出为词。
eps-free compose
首先,我们来看不包含epsilon的compose过程,其算法描述如下图所示:
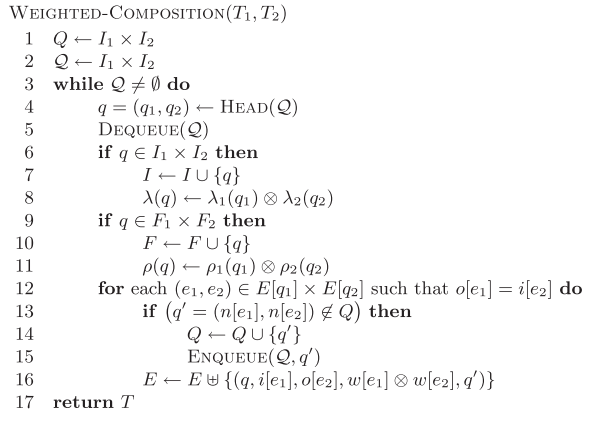
其中I表示FST的start state集合,F表示final state集合。算法中的乘号表示笛卡尔积,即叉积。 假设I1的集合为{1,2},I2的集合为{1,2,3},则I1和I2的叉积为{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)}。 该算法使用一个队列,会在开始将I1和I2的所有叉积结果(二元组)加入队列(第1行),然后开始执行一个类似广搜的过程。 二元组的表示为(q1,q2), 其中q1为FST T1中的状态,q2为FST T2中的状态。
算法的核心为第12行,从当前队列弹出一个二元组(q1,q2),当q1和q2的边(e1,e2)满足o[e1]=i[e2]时,即把(n(e1),n(e2))加入队列。 其中i(e)表示边e的输入符号,o(e)表示边e的输出符号,n(e)表示边e跳转到的下一个状态。
下图中给出给出T1和T2 compose的一个示例。
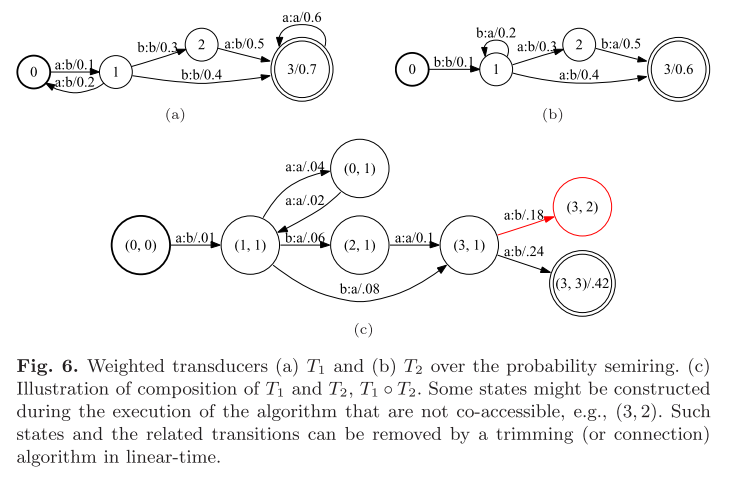
General compose
当T1和T2中包含epsilon时,需要特殊考虑。 当二元组(q1,q2)中q1含有epsilon输出边或q2中含有epsilon输入边时,分为以下三种情况。
- q1中含有epsilon输出边e时,(q1,q2)可以通过epsilon输入边跳转到(n(e),q2);
- q2中含有epsilon输入边e时, (q1,q2)可以通过epsilon输入跳转到(q1,n(e));
- q1和q2中分别时含有epsilon边输出边e1和epsilons输入边e2时,(q1,q2)则可以到达三个状态(n(e1),q2),(q1,n(e2)),(n(e1),n(e2))。
若对如下图的包含epsilon的FST T1和T2若执行上述的epsilon free compose算法时,考虑到以上三种情况,则会产生下图(a)中所示的FST(图中还可以加上由(2,1)->(3,2)输入为c输出为e的一条边)。
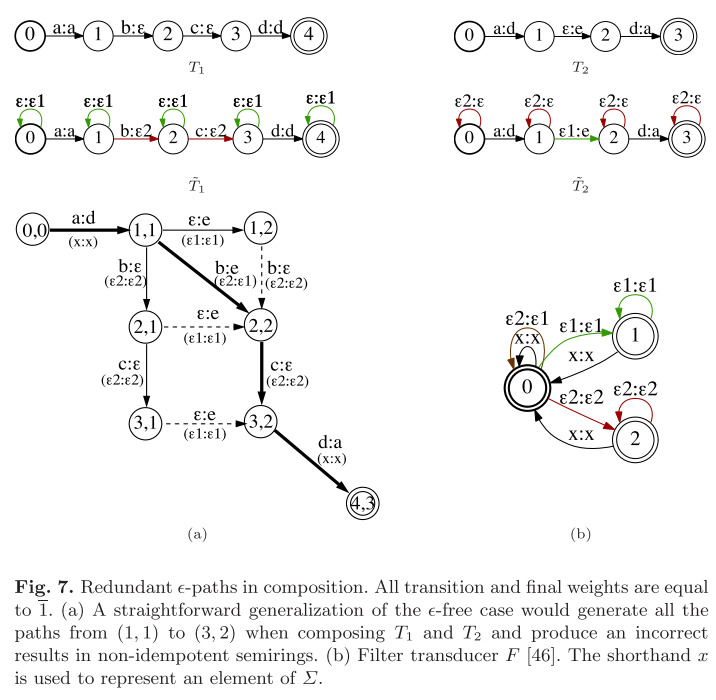
可以看到,图中由很多条含有epsilon的路径。这些路径有相同的输入序列,相同的输出序列,这就产生了冗余,而且当FST中含有由权重时,这些路径会产生不同权重的输出。
为了解决这个问题,除了一条epsilon路径外,其他的epsilon路径都要被过滤掉。也就是仅保留一条路径,而过滤掉由于$\epsilon$产生的与之相关的等价路径。 为此我们要在T1和T2中引入两个辅助符号$\epsilon1$和$\epsilon2$。 在T1中所有的状态上加上$\epsilon:\epsilon1$的自跳,将T1中边上的epsilon输出全都标记为$\epsilon2$。 在T1中所有的状态上加上$\epsilon2:\epsilon$的自跳,将T2中边上的epsilon输入全都标记为$\epsilon1$。 通过观察,我们可以制定如下四条过滤规则:
- 禁止($\epsilon2$,$\epsilon2$)后直接跟($\epsilon1$,$\epsilon1$),($\epsilon2$,$\epsilon2$)($\epsilon1$,$\epsilon1$)等价路径($\epsilon2$,$\epsilon1$)。图示中,从(1,1)到(2,1)再到(2,2)等价于从(1,1)直接到(2,2)。
- 对称的,禁止($\epsilon1$,$\epsilon1$)后直接跟($\epsilon2$,$\epsilon2$),($\epsilon1$,$\epsilon1$)($\epsilon2$,$\epsilon2$)等价路径($\epsilon2$,$\epsilon1$). 图示中,从(1,1)到(1,2)再到(2,2)等价于从(1,1)直接到(2,2)。
- 禁止($\epsilon1$,$\epsilon1$)后直接跟($\epsilon2$,$\epsilon1$),($\epsilon1$,$\epsilon1$)($\epsilon2$,$\epsilon1$)等价路径($\epsilon2$,$\epsilon1$)($\epsilon1$,$\epsilon1$)。 图示中,不存在该种情况。
- 对称的,禁止($\epsilon2$,$\epsilon2$)后直接跟($\epsilon2$,$\epsilon1$),($\epsilon2$,$\epsilon2$)($\epsilon2$,$\epsilon1$)路径($\epsilon2$,$\epsilon1$)($\epsilon2$,$\epsilon2$). 图示中,从(1,1)到(2,1)再到(3,2)等价于从(1,1)到(2,2)再到(3,2)。
举例第一条规则解释一下,假设原始compose状态为(q1,q2),($\epsilon2$,$\epsilon2$)表示T1通过含有$\epsilon$的输出边e1,T2在经过自跳转, 到达(n(e1),q2). 同理($\epsilon1$,$\epsilon1$)表示T1在自跳转, T2通过含有$\epsilon$的输入边e2,到达(q1,n(e2)); 则(q1,q2)通过($\epsilon2$,$\epsilon2$)($\epsilon1$,$\epsilon1$)可以到达(n(e1),n(e2)),然而该跳转可以通过($\epsilon2$,$\epsilon1$)一步达到,即q1经过e1输出$\epsilon$,q2经过e2输入$\epsilon$到达(n(e1),n(e2))。 同理,剩余3条规则也可以举出相应的例子。
假如从上图进行图形化的理解,($\epsilon1$,$\epsilon1$)表示向右走,($\epsilon2$,$\epsilon2$)表示向下走,先向右再向下或者先向下再向右均等价于直接从左上到右下对角线走(第1/2条规则)。 先向右走再走对角线等价于先走对角线再向右走(第3条规则)。 先向下走再走对角线等价于先走对角线再向下走(第4条规则)。 由次可见,该算法其实是一条优先走对角线的算法。
以上4条过滤规则可以构建FST $F$表示,如Fig.7中(b)图所示。最终T1和T2 Compose的结果可以表示为: \(\tilde{T1} * F * \tilde{T2}\)
在实际的实现过程中, 并不显式构建$\tilde{T1}$, $F$和$\tilde{T2}$,而是通过辅助code的技巧实现。仅需在compose的状态由二元组(q1,q2)变为(q1,q2,q3),其中q3表示filter $F$的状态,q3的取值为{0,1},0表示F跳转到了0状态上, 1表示F跳转到1或者2状态。q3的下一个状态的取值则为:
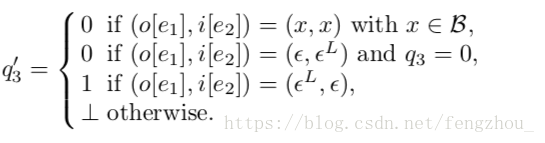
其中,otherwise表示dead state,这种情况下不会做继续扩展。
当然,我们也可以采用其他的规则做filter,上述的这种方法在Filters for Efficient Composition of Weighted Finite-State Transducers中被称作Epsilon-Sequence Filter。
算法复杂度分析
在compose算法中,最为耗时的部分为在二元组(q1,q2)中,找到满足eps-free compose算法第10行的所有(e1,e2)。 假设q1有N1条边,q2有N2条边,通过穷举的话,算法的复杂度为(N1*N2),时间复杂度很高。 Openfst通过引入Matcher,对从特定状态中查找该状态是否含有某个input/output label进行优化。
Matchers can find and iterate through requested labels at FST states; their principal use is in composition matching. In the simplest form, these are just a search or hash keyed on labels.
Matcher的基本结构为:
// Specifies matcher action.
enum MatchType {
MATCH_INPUT, // Match input label.
MATCH_OUTPUT, // Match output label.
MATCH_NONE, // Match nothing.
MATCH_UNKNOWN, // Match type unknown.
};
template <class F>
class SomeMatcher {
public:
SomeMatcher(const F &fst, MatchType type);
SomeMatcher(const SomeMatcher &matcher);
// Specifies the current state.
void SetState(StateId s);
// This finds matches to a label at the current state.
// Returns true if a match found. kNoLabel matches any
// 'non-consuming' transitions, e.g., epsilon transitions,
// which do not require a matching symbol.
bool Find(Label label);
// These iterate through any matches found:
// No more matches.
bool Done() const;
// Current arc (when !Done)
const A& Value() const;
// Advance to next arc (when !Done)
void Next();
};
// 其基本逻辑为
// 1. 通过SetState()设定要查找的状态;
// 2. 通过Find()函数查找相应的label,可能查找到多个;
// 3. 通过Value(), Next(), Done()返回查找的结果;
常见的Matcher有:
- SortedMatcher, 假设FST已经预先按照ilabel/olable进行过排序,则可以使用二分查找。这样复杂度降为O(N1•logN2)(N2>N1)或者O(N2•logN1)(N1>N2)。
- HashMatcher,直接构建哈希表(unordered_map, unordered_multimap)进行查找。Openfst中使用unordered_multimap构建以label为key,arc为value的哈希表LabelTable进行快速的查找,同时使用unordered_map构建<state, LableTable>对访问过的state进行cache。
SortedMatcher和HashMatcher的具体实现可以参考link。
Kaldi的Compose fsttablecompose中自己实现了一个TableMatcher, 对于有4条弧以下的state采用SortedMatcher,对于4条弧以上的state构建了一个vector<vector
/// TableMatcher is a matcher specialized for the case where the output /// side of the left FST always has either all-epsilons coming out of /// a state, or a majority of the symbol table. Therefore we can /// either store nothing (for the all-epsilon case) or store a lookup /// table from Labels to arc offsets
Look-Ahead Composition Filter
经典的FST Compose算法一般来说效率已经可以满足大部分的应用需求。但在一些场景下,比如FST中存在大量的输入输出为epsilon时,经典的Compose算法可能会创建了大量的无用节点(create significant numbers of non-coaccessible composition states that waste both time and space)。 比如语音识别中,H/L中均是多个输入产生一个输出,H和L中都有大量esp,L中为支持静音,也存在大量的eps的跳转。
那么如何优化该问题?类似于编译原理中的LL文法,在满足了T1的输出等于T2输入的条件下,我们可以向前多看一些状态的输入/输出来确定当前的Compose状态是否是一个有效的扩展,假设确定有效,保留当前Compose状态,反之,提前裁剪掉该状态(避免了之后对该Compose状态的无用扩展)。比如,常见的几种思想有:
-
String Potential Filter:判断通过(q1,q2)可以到达新组合出的状态($q1^{‘}$,$q2^{‘}$),从$q1^{‘}$到T1的终结点的所有输出的集合记为u, 从$q1^{‘}$到T2终结点的所有输入的集合记为v.假设u和v的交集为空集的时候,说明($q1^{‘}$,$q2^{‘}$)不能通过组合到终结点,输入无效状态。可以直接裁剪掉。该方法需要同时在T1上维护所有状态的u,在T2上维护所有状态的v。
-
Label Reachability Filter:Label Reachability filter是找T1的FST中状态q,通过任意路径到达其他任意状态$q^{‘}$的输出label集合。假设该集合有序,就可以使用2分查找预判T2中的下一个状态的输入是否在该集合中,从而确定是否要拓展。该方法仅需在T1上维护label的集合。该集合表示可以有两种。
- 点表示,即枚举有序表示该集合
- 区间表示,当该集合有序时,并且集合比较大的时,使用点表示比较浪费且查找慢。可以通过区间表示提升效率。例如{1,2,3,4,7,8,9,10}通过区间表示为{(1,4),(7,10)},不仅节省了空间,而且查找效率更高,例如点表示罚查找1二分法需要4次,而区间表示仅需要2次。区间表示法区间数量越少,则查找效率越高。
在Openfst中,使用Label Reachability Filter对Compose进行优化,并且使用区间表示集合的算法对性能优化。 该方法要求为FST中的每一个状态都构建一个上述的集合label reachability的集合。 假设FST中共有N个节点,其输出符号表的大小为M,则可以构建一个N*M的矩阵R,矩阵中第i行第j个元素表示第FST中第i个状态到达其他任意状态时是否有label为j的输出,有则R(i,j)=1,反之则为0。 在用区间表示法表示时,矩阵中每一行的1的越连续越好,矩阵中所有行的连续1的区间越少越好。该问题可以通过调换矩阵中的列去调优(即交换label的id)。 该问题被称为Consecutive One’s Property (C1P)问题,可以通过一些具体的算法结局。 在Openfst中,可以使用如下命令将普通FST转换成olabel_lookahead的FST。
fstconvert --fst_type=olabel_lookahead --save_relabel_opairs=g.irelabel.txt input.fst output.fst
Filters for Efficient Composition of Weighted Finite-State Transducers中比较了Compose时,使用各种filter的性能,如下图所示。从图中可以看出
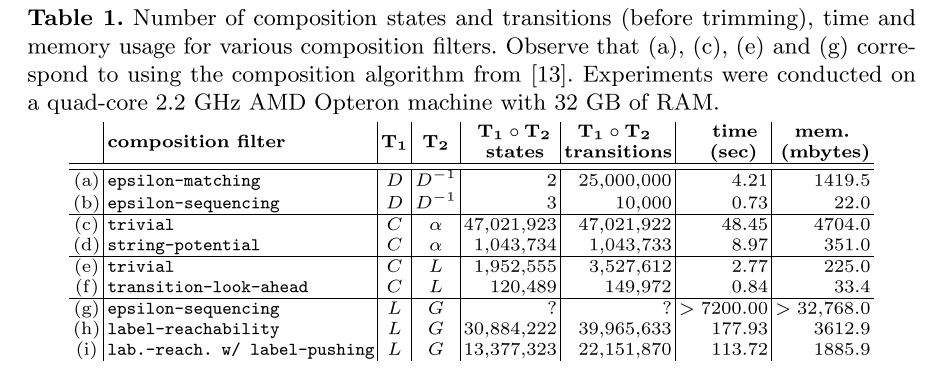
- 在一些情况下,epsilon-sequencing的算法比epsilon-matching的算法性高很多。
- 在语音识别的L*G中,Label Richability的算法性能比epsilon-sequencing更高效。
Openfst中的Compose实现
Openfst中Compose操作实现为延迟求值模式。通过ComposeFst类实现,ComposeFst类在构建时可以通过ComposeFstOptions控制相关的参数。 ComposeFstOptions中有如下几个比较重要的概念:
- Matcher
- Filter
- StateTable
其中Matcher的作用在上面已经介绍过,其功能为在Fst的状态上查找某个ilabel/olabel所对应的边Arc。
找到left Fst和right FST对应的Arc之后,Filter进一步判断当前的两个边做Compose是不是一个有效的compose状态。
A composition filter determines which matches are allowed to proceed in composition. The basic filters handle correct epsilon matching. In particular, they ensure that redundant epsilon paths, which would be incorrect with non-idempotent weights, are not created. More generally, composition filters can be used to block or modify composition paths for efficiency or other purposes usually working in tandem with specialized matchers.
Filter的基本接口如下:
template <class M1, M2>
class SomeComposeFilter {
public:
typedef typename M1::FST1 FST1;
typedef typename M1::FST2 FST2;
typedef typename FST1::Arc Arc;
// Apply filter at current composition state to these transitions.
// If an arc label to be matched is kNolabel, then that side does not consume a symbol.
// Returns the new filter state or, if disallowed, FilterState::NoState().
// The filter is permitted to modify its inputs, e.g. for optimizations.
FilterState FilterArc(A *arc1, A *arc2) const;
// Apply filter at current composition state to these final weights
// (cf. superfinal transitions). The filter may modify its inputs,
// e.g. for optimizations.
void FilterFinal(Weight *final1, Weight *final2) const;
};
Openfst中常见的Filter有SequenceComposeFilter(默认Filter)和LookAheadComposeFilter。
StateTable作用是将Compose过程中生成的状态对(元组)映射到一个新的State Id.
State tables determine the bijective mapping between state tuples (e.g. in composition triples of two FST states and a composition filter state) and their corresponding state IDs
StateTable的基本接口如下:
template <class T>
class SomeStateTable {
typedef typename T StateTuple;
// Required constructors.
SomeStateTable();
// Lookup state ID by tuple. If it doesn't exist, then add it.
StateId FindState(const StateTuple &);
// Lookup state tuple by state ID.
const StateTuple<StateId> &Tuple(StateId) const;
};
Openfst中Compose核心接口实现如下面代码所示。可以看到,ComposeFstOptions需要传递复杂的参数。在使用默认参数时, ComposeFst会根据输入fst1和fst2的性质(是left FST还是right FST,是match input还是match output,是不是lookahead的FST等)判断,自动选择合适的Matcher和Filter(CreateBase函数)。所以在不确定使用何种参数时,直接使用默认的就可以。
template <class Arc, class M = Matcher<Fst<Arc>>,
class Filter = SequenceComposeFilter<M>,
class StateTable =
GenericComposeStateTable<Arc, typename Filter::FilterState>>
struct ComposeFstOptions : public CacheOptions {
M *matcher1; // FST1 matcher.
M *matcher2; // FST2 matcher.
Filter *filter; // Composition filter.
StateTable *state_table; // Composition state table.
explicit ComposeFstOptions(const CacheOptions &opts = CacheOptions(),
M *matcher1 = nullptr, M *matcher2 = nullptr,
Filter *filter = nullptr,
StateTable *state_table = nullptr)
: CacheOptions(opts),
matcher1(matcher1),
matcher2(matcher2),
filter(filter),
state_table(state_table) {}
};
ComposeFst(const Fst<Arc> &fst1, const Fst<Arc> &fst2,
const CacheOptions &opts = CacheOptions())
:ImplToFst<Impl>(CreateBase(fst1, fst2, opts)) {}
// Create compose implementation specifying no matcher type.
static std::shared_ptr<Impl> CreateBase(const Fst<Arc> &fst1,
const Fst<Arc> &fst2,
const CacheOptions &opts) {
switch (LookAheadMatchType(fst1, fst2)) { // Check for lookahead matchers
default:
case MATCH_NONE: { // Default composition (no look-ahead).
ComposeFstOptions<Arc> nopts(opts);
return CreateBase1(fst1, fst2, nopts);
}
case MATCH_OUTPUT: { // Lookahead on fst1.
using M = typename DefaultLookAhead<Arc, MATCH_OUTPUT>::FstMatcher;
using F = typename DefaultLookAhead<Arc, MATCH_OUTPUT>::ComposeFilter;
ComposeFstOptions<Arc, M, F> nopts(opts);
return CreateBase1(fst1, fst2, nopts);
}
case MATCH_INPUT: { // Lookahead on fst2
using M = typename DefaultLookAhead<Arc, MATCH_INPUT>::FstMatcher;
using F = typename DefaultLookAhead<Arc, MATCH_INPUT>::ComposeFilter;
ComposeFstOptions<Arc, M, F> nopts(opts);
return CreateBase1(fst1, fst2, nopts);
}
}
}
// Identifies and verifies the capabilities of the matcher to be used for
// lookahead with the composition filters below. This version is passed two
// matchers.
template <class Matcher1, class Matcher2>
MatchType LookAheadMatchType(const Matcher1 &m1, const Matcher2 &m2) {
const auto type1 = m1.Type(false);
const auto type2 = m2.Type(false);
if (type1 == MATCH_OUTPUT && m1.Flags() & kOutputLookAheadMatcher) {
return MATCH_OUTPUT;
} else if (type2 == MATCH_INPUT && m2.Flags() & kInputLookAheadMatcher) {
return MATCH_INPUT;
} else if (m1.Flags() & kOutputLookAheadMatcher &&
m1.Type(true) == MATCH_OUTPUT) {
return MATCH_OUTPUT;
} else if (m2.Flags() & kInputLookAheadMatcher &&
m2.Type(true) == MATCH_INPUT) {
return MATCH_INPUT;
} else {
return MATCH_NONE;
}
}